Поиск материалов, просьбы о помощи... Опции

[Cтранник]

Bukich, офигеть. У кого ж столько свободного халявного времени будет?
В производных вообще ничего сложного нет. Есть таблицы простейших производных - они качаются с инета, либо записываются на лекциях\смотрятся в книгах. Затем есть правило, что d(u(y(x)))\dx=du\dx*dy\dx (частные пр.) Т.е. производная от сложной функции есть произведение производных. К примеру, есть ф-ия (sinx)^2. Производная синуса есть cosx, а частная производная функции t^2 есть 2t, где t считаем ф-ией, не зависящая от х(поскольку производная частная), t=sinx, то есть получается 2sinx. Итого производная исходной ф-ии есть 2sinx*cosx.
Точно также поступаем, если пользуемся другими правилами взятия производной - производная от произведения, или производная от частного.

Во взятии пределов пос-тей есть также несколько простых правил:
1) Пределы считают тогда, когда имеют какого-то вида неопределённость в выражении под пределом. Например, 0 или бесконечность делить на бесконечность. lim(3*n^2+1\2-n^2) при подставлении вместо n бесконечности получим бесконечность делить на бесконечность. Непонятно, что с этим делать. Задача состоит в том, чтобы при подстановке не возникало неопределённости, т.е. был бы 0, бесконечность, или какая-то константа. Вся задача сводится к упрощению выражения под пределом.
2) Для выражений дробей с многочленами. Делим на макс. степень величины, одупляем получившееся. Т.е. если есть lim(3*n^2+1\2-n^2), макс. степень - вторая, делим на n^2 числитель и знаменатель: lim(3+1/n^2/2/n^2-1), очевидно, что те величины, которые поделены на n^2 при устрелмение n к бесконечности дают 0. Значит предел 3\-1
Все задания про последовательности в том листе на это правило. Кроме третьего, там, где разность корней. Когда есть такая хрень, думают, как сделать так, чтобы оно попроще было, то есть снова свести к дроби. Обычный выход - домножить на сопряжённое. Т.е. таким образом, чтобы получилась разность квадратов, или квадрат (по обстоятельствам). Т.е. на (n+1)^1\2-n^1\2. Раз домножаем на это выражение, то и делим на него. В результате в чистителе получилось выражения вида (a-^2=a^2-2ab+b^2. В знаменателе то, что писал выше. И поступаем, как с обычной дробью.
3) Особенность функций состоит в том, что здесь больше поля для действий и озадачивания студента. В отличие от последовательности, x можно устремлять куда угодно: к бесконечности, к нулю, к константе. Соотвественно, многие приёмы строятся именно на перестановке пределов. Есть ещё замечательные пределы: limsinx\x=1 при x->0, lim(1+1\x)^x->1 при x->беск.
Все задания там на эти пределы. По возможности надо увидеть тот или иной предел и с помощью замены свети выражение к этому пределу. Или снова к дроби.
4) Есть также для дробей правило Лапиталя. Состоит в том, что limf(x)\g(x)=limf'(x)\g'(x). Т.е. предел от частного функций равен пределу от частного производных функций. Очень удобно, пользуйтесь. Хорошо работает на всякие степени, сложности возникают с тригонометрией.
5) Правило Лапиталя есть фундаментальное обобщение всех пределов. Производная это фактически скорость возрастания функции. Совершенно очевидно, что естьу нас есть разность двух ф-ий, пусть каждая из них стремится к беск-ти - какая-то может быстрее к ней стремиться, какая-то медленее. Это приводит к выводу. что можно очень просто проверять все результаты. К примеру, дан предел е^x-x при x к беск-ти. Очевидно, что e^x растёт быстрее, чем линия. А значит предел будет равен беск-ти. Если дана дробь с многочленами, предел будет равен нулю или беск-ти в зав-ти от того, где выше степень - в числителе или в знаменателе. Отдельный случай, когда они равны - сложно будет сказать точно.
Для справки: ...1\x...lnx..x^1\2,...x...x^2...e^x..x!...x^x.. в порядке возрастания при x-> беск-ти
С уважением,
Astart

Сообщение отредактировано Cтранник - 25.01.2009 - 19:07

[Mystmuse]

Как можно заполучить пакет Statistica? Без "пожертвований"...

[Kreon]

Как можно заполучить пакет Statistica? Без "пожертвований"...

Смотря какую версию. Что-то более ли менее современное (версия 7.0) есть у меня в DC++.
В миэте на тех лабах, где лично я сталкивался с этой программой, использовалась жутко доисторическая версия, которая нормально работает только под Windows 95/98. Под 2000/XP и выше вылетает так, что никакой режим совместимости от этого не помогает. Хотя если сильно надо - могу и её найти и выложить.

[pecherkin]

Как можно заполучить пакет Statistica? Без "пожертвований"...

Неудержусь и скажу качай в ДЦ вот у меня она точно там есть версия 6
Я лично когда делал по этой проге работы по статистическому анализу юзал старую версию как раз ту о которой расписано в книжке Вуколова ну это как минимум у меня так было.
Сейчас в инете есть рабочие версии Statistica (v.5.5A) (6.0) (8 MR-3)

Сообщение отредактировано pecherkin - 11.03.2009 - 23:43

[Mystmuse]

Спасибо, тащу.

[vasyatimonovo]

сколько будет lg 414?и как посчитать?часть мозга,отведённой под математику,заправлена тормозной жидкостью.
расскажите как пользоваться таблицой брадиса!

Сообщение отредактировано vasyatimonovo - 25.03.2009 - 20:55

[Cтранник]

Маткад, матлаб, инженерный калькулятор в винде(пендосы log без основания считают lg), другие виды калькуляторов, вспомогательные срества SLW, для особо извращенных личностей разложение в ряд ручками.
2,617
Таблицы Брадиса давно потеряли свою актуальность. В прошлое, когда не было всего описанного выше, надо было как-то проводить достаточно объёмные операции умножения и, в особенности, деления. Вышли из ситуации просто: используя обыкновенные св-ва логарифмов, loga\b=loga-logb. Отсюда лекго восстановить a\b. Для этого и были составлены таблицы Брадиса. Сейчас они уже своё удобство, наверное, потеряли.
Но на всякий случай, выдержка из какой-то умной книжки:

таблицы Логарифмов чисел; применяются для упрощения вычислений. Наиболее распространены таблицы десятичных логарифмов. Т. к. десятичные логарифмы чисел N и 10kN (при k целом) различаются только характеристиками и имеют одинаковые мантиссы (lg10kN = k + lg N), то в таблицах десятичных логарифмов приводятся только мантиссы логарифмов целых чисел. Для отыскания характеристики служат правила: 1) характеристика числа, большего 1, на единицу меньше числа цифр в целой части этого числа (так, lg 20 000 = 4,30103) и 2) характеристика десятичной дроби, меньшей 1, равна взятому со знаком минус числу нулей, предшествующих первой в дроби цифре, отличной от нуля (так, lg 0,0002 = - 4,30103, т. о., десятичные логарифмы дробей записываются в виде суммы положительной мантиссы и отрицательной характеристики).

С уважением,
Astart

[Юлия 52]

Ребят если есть время помогите пожалуйста решить примеры по диффурам,или хотя бы идею киньте.
1) решить уравнение ,допускающее понижение порядка у"=1/у^1\2
2)ршить уравнени 1-го порядка
(х+2у)у'=1, у(0)= -1
№3)и вопрос как взять интеграл от (9х^2+6x+2)/x^3*e^3x
Буду признательна если поможите.срочно очень надо

Сообщение отредактировано Юлия 52 - 6.05.2009 - 18:19

[Cтранник]

Добрый вечер. Я не математик, но кое-что умею. Например, нумерацию изменять)
2) Алгоритм решения:
а) замена y'=p, где p - некоторый параметр. Подстановка замены в уравнение, затем выражаем y. Получается y=1\2p-x\2.
б) возвращаемся к y'=p, дифференцируем получившийся y из первого пункта по х, учитывая, что р также ф-ия х. Получается p=-1\2+dx\2dp.
в) решаем это уравнение простейшим методом разделения переменных. Получается x=p^2+p+c.
г) Записываем ответ в виде системы y из пункта а) и x из пункта в).
д) Подставляем х=0 в уравнение с y, вычисляем p. Подставляя x=0 и полученное p в уравнение с х, считаем с.
Всё. Замечание: представление ответа в виде системы является нормальным. Иной раз это даже единственно возможный вариант представления ответа.
1) Ах, да. В вопросе 2) мы именно понижали порядок, вводя такую замену. Поэтому этот метод получил название метода понижения порядка. Т.е. алгоритм см. выше.
3) Если дифференциал х, то тогда почленным делением на 3 дроби. Потом по ф-ле Udv=UV-VdU. Очень, конечно, не хочется, чтобы вы считали ещё много интегралов, но иного пути я не вижу. Может быть, можно ввести какую-нибудь хитрую замену, но что-то не просматривается. Хотя по ответу видно, что должен быть способ проще.
Ответ будет (3x+1)/x^2*e^3x.
Если до завтра терпит, то закину в голову на ночь, она что-нибудь придумает, а то вечно я работаю)
С уважением,
Astart

[Юлия 52]

Добрый вечер. Я не математик, но кое-что умею. Например, нумерацию изменять)
2) Алгоритм решения:
а) замена y'=p, где p - некоторый параметр. Подстановка замены в уравнение, затем выражаем y. Получается y=1\2p-x\2.
б) возвращаемся к y'=p, дифференцируем получившийся y из первого пункта по х, учитывая, что р также ф-ия х. Получается p=-1\2+dx\2dp.
в) решаем это уравнение простейшим методом разделения переменных. Получается x=p^2+p+c.
г) Записываем ответ в виде системы y из пункта а) и x из пункта в).
д) Подставляем х=0 в уравнение с y, вычисляем p. Подставляя x=0 и полученное p в уравнение с х, считаем с.
Всё. Замечание: представление ответа в виде системы является нормальным. Иной раз это даже единственно возможный вариант представления ответа.
1) Ах, да. В вопросе 2) мы именно понижали порядок, вводя такую замену. Поэтому этот метод получил название метода понижения порядка. Т.е. алгоритм см. выше.
3) Если дифференциал х, то тогда почленным делением на 3 дроби. Потом по ф-ле Udv=UV-VdU. Очень, конечно, не хочется, чтобы вы считали ещё много интегралов, но иного пути я не вижу. Может быть, можно ввести какую-нибудь хитрую замену, но что-то не просматривается. Хотя по ответу видно, что должен быть способ проще.
Ответ будет (3x+1)/x^2*e^3x.
Если до завтра терпит, то закину в голову на ночь, она что-нибудь придумает, а то вечно я работаю)
С уважением,
Astart

Извини что так долго не отвечала)))да терпит даже до четверга))))спс за идеи))проработаю)))
надумали что нибудь с интегралом?и ещё вопрос.когда решали 2 номер почему при дифф.получилось p получилось такое.разве там не так p=-1/2-1/p^2

Сообщение отредактировано Юлия 52 - 11.05.2009 - 21:06

[Cтранник]

К четвергу может надумаю. А может и не надумаю. Советую всё же посчитать множество интегралов, может таким образом решение более короткое в голову придёт.
Дифференциируем в номере 2 в том пункте мы по х, а не по p. Но поскольку р также функция х, то возникает dp\dx, а т.к. p изначально было в знаменателе, то это переворачивается в dx\dp
С уважением,
Astart

[Юлия 52]

К четвергу может надумаю. А может и не надумаю. Советую всё же посчитать множество интегралов, может таким образом решение более короткое в голову придёт.
Дифференциируем в номере 2 в том пункте мы по х, а не по p. Но поскольку р также функция х, то возникает dp\dx, а т.к. p изначально было в знаменателе, то это переворачивается в dx\dp
С уважением,
Astart

Всё спс)))втрой номер мне уже помогли.во 2 мы сделали по другому.и всё оказалось оченьлегко)) и с интегралом тоже разобрались)))
но всё равно большое спасибо за потраченное время и усилия)))

Сообщение отредактировано Юлия 52 - 16.05.2009 - 22:09

[Юлия 52]

Здравствуйте.теперь возникла проблема с матаном.Кто в этом что-нибудь понимаете помогите плиз.или хотя бы ваши идеи и предположения.Задание 2 не нужно смотреть,уже сделала.

Прикрепленные файлы

 CCI00016.zip ( 370.46 килобайт ) Кол-во скачиваний: 7

 

[Mystmuse]

Люди, выручайте, не могу найти ответы на следующие вопросы:

5. Назовите страны Восточной Европы, добившиеся наибольших успехов в рыночных преобразованиях. С чем это связано?
7. Назовите уровни мировой торговли.
8. Перечислите общие принципы приватизации в Восточной Европе.
10.Какие группы факторов влияют на научно-технический потенциал страны.


Сообщение отредактировано Mystmuse - 20.05.2009 - 18:18

[Cтранник]

1. По частям, с U=sqrt(1-x^5), V=x^3\2. Это реккуретный интеграл, в процессе его подсчёта будут возникать похожие на него интегралы, тогда их просто следует переносить в левую часть. Как все подобные перенесутся, в левой части будет некий коэффициент, на который надо будет поделить всё выражение.
Если владеете вычетами - то там проще. Хотя по программе видно, что, наверное, ещё не владеете.
3. Через двойной интеграл. Строите кривые, ищите точки пересечения. Потом смотрите, откуда до куда бежит х, откуда до куда бежит у - этим самым определяете пределы интегрирования.
Если двойной интеграл ещё не знаком - ищите точки пересечения, считаете площадь под каждым графиком отдельно с помощью определённого интеграла (точки пересечения дадут пределы интегрирования), потом прибавляете\вычитаете по обстоятельствам.
4,5 где сложности-то? Если были бы конкретные наработки и вопросы, можно бы было говорить конкретные слова. А так - считаете интеграл по частям или домножением на сопряжённое, подставляете предел, считаете предел. Всё.
6. Вот здесь нюанс.
Сначала на абсолютную. Берём модуль от подынтегрального выражения, пишем, что синус не превосходит единицы. Значит всё выражение лежит между 0 и х^2. Поскольку интеграл от dx\x^2 сходится, степень равна двум, то и модуль функции, ограниченный сверху и снизу, следовательно, также сходится абсолютно.(по признаку двух ментов и одного бухого. Куда они его ведут, туда он и идёт).

10. Не знаю, что там у экономистов, но мнение рядовых тружеников этой стези: большое количество хорошего и дешёвого алкоголя. Ещё установочки всякие, с лампочками. Чем больше лампочек, тем лучше.

С уважением,
Astart

Сообщение отредактировано Cтранник - 20.05.2009 - 19:46

[Mansoor]

Если кто может помочь с курсовой по таможенному делу - пишите в личку.

[Мохнатый]

Помогите посчитать пожалуйста интеграл от 0 до 2*pi от 1/(0.5+0.3*cos(x)).^2
Тема теория функци комплексной переменной.

[Cтранник]

Подобные интеграля сводятся к интегралу по замкнутому контуру - окружности, через замену z=e^(ix). Соотвественно dz=ie^(ix)dx=izdx. => dx=dz\iz. Cosx=(e^-ix+e^ix)/2=(z+1\z)/2. Произведя такую замену, меняют пределы интегрирования на модуль z=1 (двигаемся от 0 до двух пи с точки зрения комплексной плоскости - двигаемся по окружности радиуса 1). Ну а дальше по схеме расчёта интеграла через вычеты: подобный интеграл равен 2пиi сумма вычетов по точкам, входящим в область интегрирования.
С уважением,
Astart

Сообщение отредактировано Cтранник - 25.05.2009 - 21:11

[CTAJIuH]

Помогите пожалуйста, никак не могу справиться с 2 номерами БДЗ


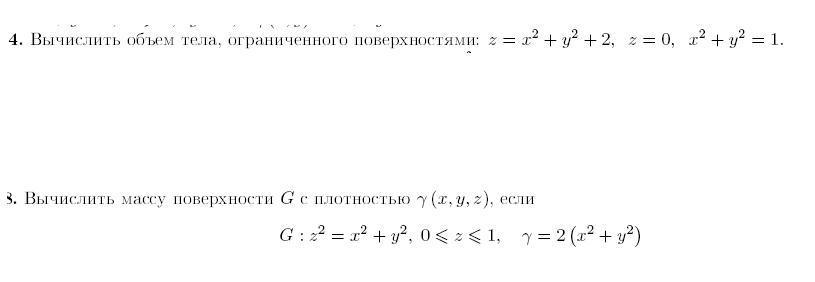в 4 никак немогу области интегрирования поставиьт правильно+рисунок..
в 8 аналогично.
Буду благодарен если мне напишут интегралы

заранее спасибо)

[carniton]

кто-нибудь в схемотехнике рубит?